Laplacian of Gaussian (LoG)As Laplace operator may detect edges as well as noise (isolated, out-of-range), it may be desirable to smooth the image first by convolution with a Gaussian kernel of width
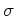
to suppress the noise before using Laplace for edge detection:
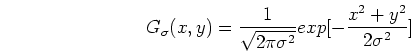
The first equal sign is due to the fact that
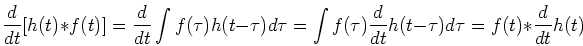
So we can obtain the Laplacian of Gaussian
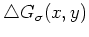
first and then convolve it with the input image. To do so, first consider
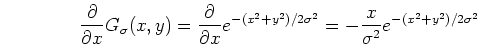
and
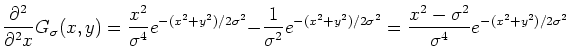
Note that for simplicity we omitted the normalizing coefficient
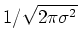
. Similarly we can get
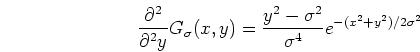
Now we have LoG as an operator or convolution kernel defined as
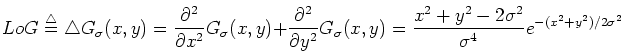
The Gaussian
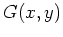
and its first and second derivatives
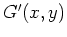
and
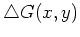
are shown here:
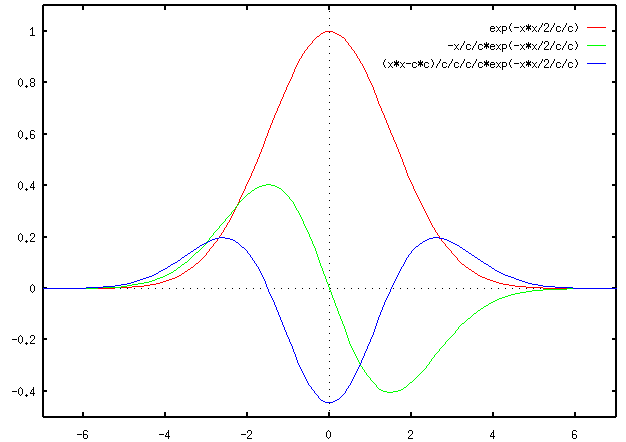
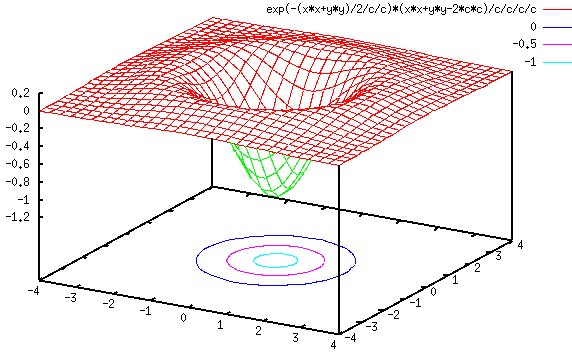
This 2D LoG can be approximated by a 5 by 5 convolution kernel such as
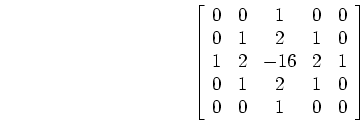
The kernel of any other sizes can be obtained by approximating the continuous expression of LoG given above. However, make sure that the sum (or average) of all elements of the kernel has to be zero (similar to the Laplace kernel) so that the convolution result of a homogeneous regions is always zero.
The edges in the image can be obtained by these steps:
Applying LoG to the image
Detection of zero-crossings in the image
Threshold the zero-crossings to keep only those strong ones (large difference between the positive maximum and the negative minimum)
The last step is needed to suppress the weak zero-crossings most likely caused by noise.
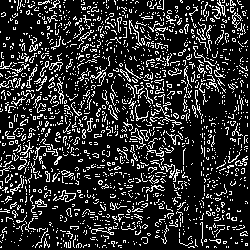
http://www.codeproject.com/KB/GDI-plus/Laplace_Gaussion_edge.aspx
http://www.codeproject.com/KB/GDI-plus/Image_Processing_Lab.aspx
http://fourier.eng.hmc.edu/e161/lectures/gradient/node10.html